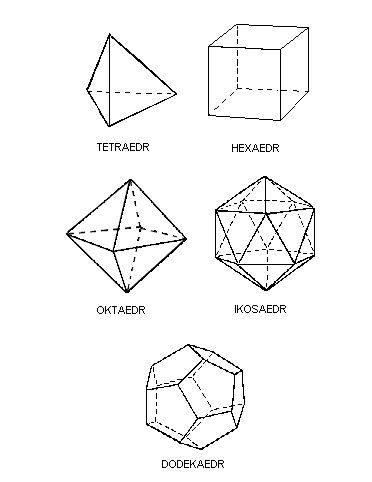
Pět Platónových těles
Platónova tělesa
Pravidelný mnohoúhelník má všechny strany stejně dlouhé a všechny úhly stejně
velké. Lze mu opsat i vepsat kružnici. Obdobou pravidelných mnohoúhelníků v
rovině jsou v prostoru pravidelné mnohostěny. Pravidelný mnohostěn je takový
mnohostěn, jehož všechny stěny jsou shodné pravidelné n-úhelníky, a v každém
jeho vrcholu se stýká stejný počet m hran.
Připomeňme si také, že pro každé celé číslo n ≥ 3 existuje
pravidelný n-úhelník. Jistě by bylo možné předpokládat, že obdobně pro každé
celé číslo n ≥ 4 by měl existovat pravidelný n-stěn. Ale není tomu
tak. Pravidelných mnohostěnů, samozřejmě pokud máme na zřeteli jen jejich tvar
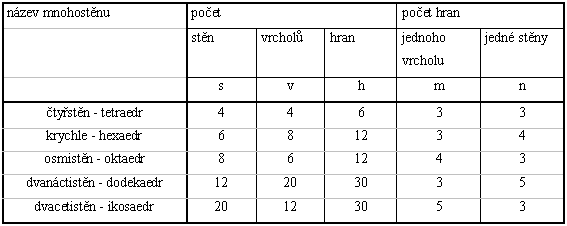
a nikoliv velikost, známe pouze pět. Které to jsou, vyplývá z tabulky.
Zajímavé je, že těchto pět pravidelných mnohostěnů znali již starořečtí
matematici počátkem 4.století př.n.l. Řecký filozof Platón (427-347 př.n.l.)
jich dokonce používal k objasňování svého učení o podstatě hmotného světa tím,
že krychli, osmistěn, čtyřstěn a dvacetistěn považoval za představitele čtyř
základních živlů, jimiž byly podle jeho učení země, vzduch, oheň a voda, a
dvanáctistěn za představitele jsoucna neboli všeho, co existuje.
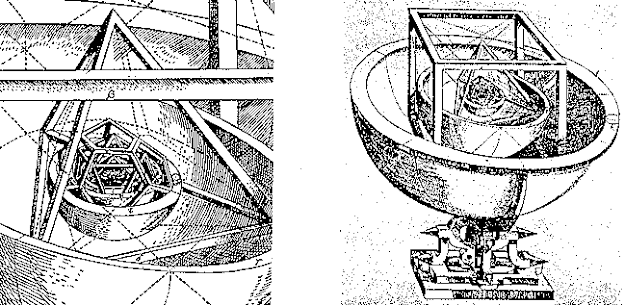
Podobně bychom mohli rozvést i učení známého hvězdáře Johanna Keplera
(1571-1630), podle něhož se tehdy šest známých planet pohybovalo okolo Slunce
po kulových plochách vepsaných nebo opsaných pravidelným mnohostěnům.
Například Země obíhá po kulové ploše procházející středy stěn pravidelného
dvanáctistěnu (vepsaná kulová plocha) a Mars po kulové ploše procházející
vrcholy pravidelného dvanáctistěnu (opsaná kulová plocha). Tuto Keplerovu
teorii rozbil fakt, že vzájemná vzdálenost kulových ploch neodpovídala
skutečným vzdálenostem planet od Slunce. Kromě toho známe dnes další tři
planety: Uran, Neptun a Pluto.
Jak je možné, že pravidelných mnohostěnů je právě pět. Není možné, že jsme
tvary některých mnohostěnů zatím neobjevili? Dokažme si, že tomu tak není.
Pro pravidelné mnohostěny můžeme odvodit vztah
kde je počet hran jednoho vrcholu a n ≥ 3 počet hran jedné stěny.
Vyřešíme nerovnici pro všechna celá čísla m ≥ 3 a n ≥ 3.
Řešením jsou pouze hodnoty uvedené v tabulce o mnohostěnech.
Nejjednodušší mnohostěn má roh tvořený třemi rovnostrannými trojúhelníky,
další jich mají čtyři nebo pět. Šest rovnostranných trojúhelníků s jedním
společným vrcholem poskládáme do roviny, takže nemohou tvořit povrch
mnohostěnu. Stejné to bude, když spojíme čtyři čtverce. Podobně tři pravidelné
pětiúhelníky v jednom vrcholu jsou maximum. Šestiúhelníky a mnohoúhelníky s
více než šesti stranami jsou také vyloučeny.
V 18.století formuloval Leonard Euler (1707-1783) vztah pro každý konvexní
mnohostěn:
vztah mezi počtem vrcholů v, hran h a stěn s. Byl to empirický objev získaný
pozorováním, kterému vyhovují i údaje uvedené v naší tabulce pro pravidelné
mnohostěny.
Jistě jste si v tabulce všimli této symetrie:
O krychli a osmistěnu říkáme, že jsou duální mnohostěny. Všimněte si, že
středy stěn krychle jsou vrcholy pravidelného osmistěnu a naopak středy stěn
pravidelného osmistěnu jsou vrcholy krychle. Podobně jsou navzájem duální i
pravidelný dvanáctistěn a pravidelný dvacetistěn. Pravidelný čtyřstěn je
duální sám se sebou.
Zkusme uvažovat, proč byl právě dvanáctistěn oblíbenou hračkou etruských dětí
před 2500 lety, jak ukázaly vykopávky v Monte Loffa u Padovy. Pythagorejcům
mohl být znám pravidelný osmistěn a dvanáctistěn - dvanáctistěn proto, že v
tomto tvaru krystalizují pyrity vyskytující se v Itálii a že s modely takových
tvarů jako s ornamenty nebo s magickými symboly se setkáváme právě u Etrusků.
Krychle a čtyřstěn také slouží lidem při jejich budovatelském úsilí i
hráčských vášních. Dosvědčují to dětské kostky i konstruktivistická
architektura. Proč má hrací kostka z Ptolemaiovy doby vystavená v
egyptologických sbírkách Britského muzea právě tvar dvacetistěnu? Proč se od
dávných dob až po naše časy užívají svítilny ve tvaru pravidelného osmistěnu,
i když jejich vnitřek prodělal vývoj od svíčky k výbojce?
Pěti pravidelným mnohostěnům se ve své knize "O božském poměru" věnuje i jeden
z nejvýznamnějších matematiků své doby Luca Pacioli (1445-1514). Kniha nazvaná
podle "zlatého řezu" byla podle Vitruvia věnována architektuře, pěti
Platonovým tělesům a také proporcím lidského těla. Vyobrazení mnohostěnů na 59
tabulkách pro svého přítele zhotovil Leonardo da Vinci, který si s oblibou
vyráběl dřevěné kostry mnohostěnů.
Co božského našel na pěti jednoduchých tělesech Luca Pacioli, který žil více
než dva tisíce let po Platonovi? Je to jen ozvěna Platonova okřídleného rčení
"Bůh činí vždy geometricky"? Nikoliv, mnich Luca Pacioli myslil realističtěji:
Bůh se jako geometr neprojevuje vždy, ale jen někdy. Zejména v případě tzv.
zlatého řezu. Pacioli zjistil, že je třináct projevů této božské proporce, a
hledal je v nejdokonalejších matematických výtvorech, pěti platonovských
tělesech. Zhotovil je ze skleněných destiček a věnoval různým velmožům do
jejich sbírek. Kapitola "O dvanácté, téměř nadpřirozené vlastnosti" pojednává
o pravidelném dvacetistěnu.
Podívejme se na tuto dávnou hrací kostku pozorněji. V každém vrcholu se
stýká pět trojúhelníků a jejich třetí strany tvoří pravidelný pětiúhelník.
Spojíme-li dvě protilehlé hrany dvacetistěnu, dostaneme obdélník, který také
bezprostředně souvisí s božskou proporcí: Jeho delší strana je k menší ve
stejném poměru jako součet stran k delší.
Dvanáct vrcholů dvacetistěnu tedy tvoří dvanáct vrcholů tří zlatých
obdélníků, které leží ve třech navzájem kolmých rovinách.
Jeho model tedy můžeme jednoduše udělat ze tří stejných čtvrtek papíru s
poměrem stran j. Jejich společný průsečík je střed dvacetistěnu. Hrany,
které se protínají v jednom vrcholu tohoto tělesa, náleží pravidelnému
pětibokému jehlanu, jehož podstavu tvoří strany zlatého obdélníku, jehož
delší strana je uhlopříčkou pravidelného pětiúhelníku tvořícího podstavu
jednoho z jehlanů.
Dvacetistěn souvisí s ještě jednou matematickou perličkou, problémem
líbajících se koulí, který se stal předmětem sporu Isaaca Newtona s
oxfordským astronomem Davidem Gregorym.
Newton nedokázal Gregoryho přesvědčit, že maximální počet shodných koulí,
které se všechny dotýkají jedné další s nimi shodné koule, je nanejvýš
třináct včetně koule líbané.
Škoda, že se tenkrát ještě nehrál pingpong, mohli si udělat pokus. Bez
ohledu na pověry vzít třináct míčků a stáhnout je průhlednou gumovou blánou.
Přesvědčili by se, že dvanáct koulí se rozmístí do vrcholů pravidelného
dvacetistěnu a obklopí třináctou. Mezi nimi však zůstane trochu vůle. Je
dost velká, aby se tam vmáčkla ještě čtrnáctá koule? O to vlastně jde. Koule
můžeme všelijak přeskupovat, ale pro čtrnáctou se místo neuvolní.
Ale i ostatní mnohostěny mají mnoho zajímavých vlastností:
Osmistěn. Dvacetistěn může být vepsán do osmistěnu tak, že každý vrchol
dvacetistěnu rozdělí hrany osmistěnu v poměru zlatého řezu.
Dvanáctistěn. Vepíšeme-li do pravidelného dvanáctistěnu tři navzájem kolmé
zlaté obdélníky, budou jejich vrcholy ležet ve středech dvanácti
pětiúhelníkových ploch.
Estetické působení těchto těles nemůžeme ničím vysvětlit, avšak skutečnost,
že tato tělesa byla užívána po celé generace lidstva, je dostatečným
důkazem.